小学4年の算数問題が分からなくてヘコんだわの解き方

ネットで、今週出回っていた、算数の図形問題。

「大きさのちがう３つの正方形をならべて、下のような図形をつくりました。この形の面積は何cm²ですか」

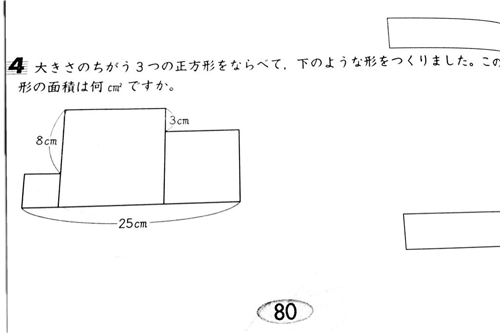
X、連立方程式をつかうのはダメで、一見難しそうで、大人でもお手上げみたいなところなんだけど、塾に通っている子たちには、そうでもないのかなあと。
小５の長男と一緒に解いてみました。

図形問題で、こういうシンプルになっている場合、ヒントとなるのは、

「どの部分が同じか」

ということを第一に考えてみます。

この場合、キモになるのは、正方形が３つということ。なので、各辺の長さは同じ。
そして、長さがわかっている部分に注目してみる。特に25cmのところは、ここだけ長さがわかっているのは唐突感があって無茶苦茶あやしいので、ここを分解できないかと考えてみます。

そうすると、

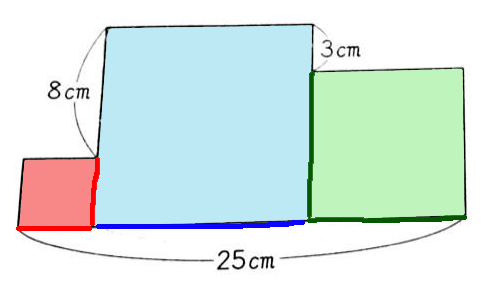
この図のように、小サイズ(赤)の正方形の赤色の辺の長さ、中サイズの正方形(緑)の緑色の辺の長さは、等しい。

赤の長さ＋青の長さ＋緑の長さ＝25cm

を使って、中央の大サイズの正方形に注目してみると、

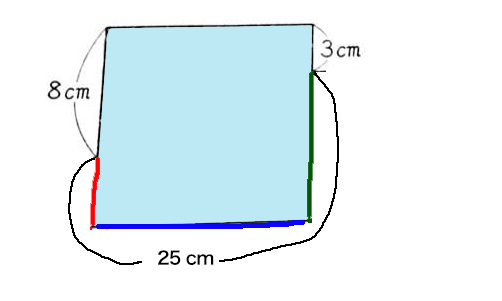
ここまでわかると、大サイズ(青)の正方形の３辺に注目して、3辺の合計の長さがわかるから、３辺の各辺の長さは正方形で同じなので、

　(8+25+3)÷3=12

12cmが大サイズの正方形の1辺の長さとなる。

よって、小サイズ(赤)の正方形の1辺の長さは

12-8=4

4cm

中サイズ(緑)のの正方形の1辺の長さは

12-3=9

9cm

したがって、図形の面積は

4×4 ＋ 12×12 ＋ 9×9 = 241

241cm²

となる。他にも同じ解き方をされていた方がいましたので、これであっているかと。

日能研全国1位、さすがです！

こういうのは、受験テクニック的なものなんでしょうか？